portfolio
PUBLIC如果想要理解投资,应该从哪里开始?
关于投资的论断经常和一些似是而非的词关联在一起:“认知”,“心性”,“信仰”。
如果在某个瞬间觉得这种描述过于主观,有没有solid一些的理论可以用?
我意识到写这一篇内容的目的,是最符合我做这个site的初心的。
那就是,如果你也关心这个内容,请务必let’s_have_a_talk。
我们的loss function是什么
我们要通过portfolio获得什么。
最大收益?
可能是,如果两个组合收益相同,但是波动一个大一个小呢?
最小波动?
可能是,如果你是养老基金,可能需要一个最小波动的组合,并惊讶地发现,这个最小波动的组合甚至可以从市场中性中获益。
收益/波动?
可能是,简单地定一个函数Sharpe Ratio:收益/波动。但是为什么不是收益/两倍波动?
给定波动,最大化收益?
可能是,类似于银行给大家做过的投资者资格测试,你能承担的最大损失是多少。潜台词就是可接受的最大损失,决定了portfolio,进而决定了最大收益。
portfolio 101
一切从如下直觉开始。
我们知道如果 \(A\) 是\(N(u, \sigma^2)\),\(B\) 也是\(N(u, \sigma^2)\),(并且可耻地假设 \(cov(A,B) = 0\) )。
那么 \(\frac{1}{2}A+\frac{1}{2}B\) (对应各买一半)则是 \(N\left((u+u)/2, (\frac{\sigma}{2})^2+(\frac{\sigma}{2})^2\right) = N\left(u, \frac{1}{2}\sigma^2\right)\),收益 \(u\) 不变,风险从 \(\sigma\) 变成了 \(\frac{1}{\sqrt{2}}\sigma\)。
更进一步地。
如果A,B不是i.i.d.,但是我们知道 \(cov(A,B) = \Sigma\) ,我们是不是可以获得一个连续的变换,获得不同的portfolio,也就是不同的(收益,波动)表现的组合。
这种方法就是所谓的Portfolio Optimization。
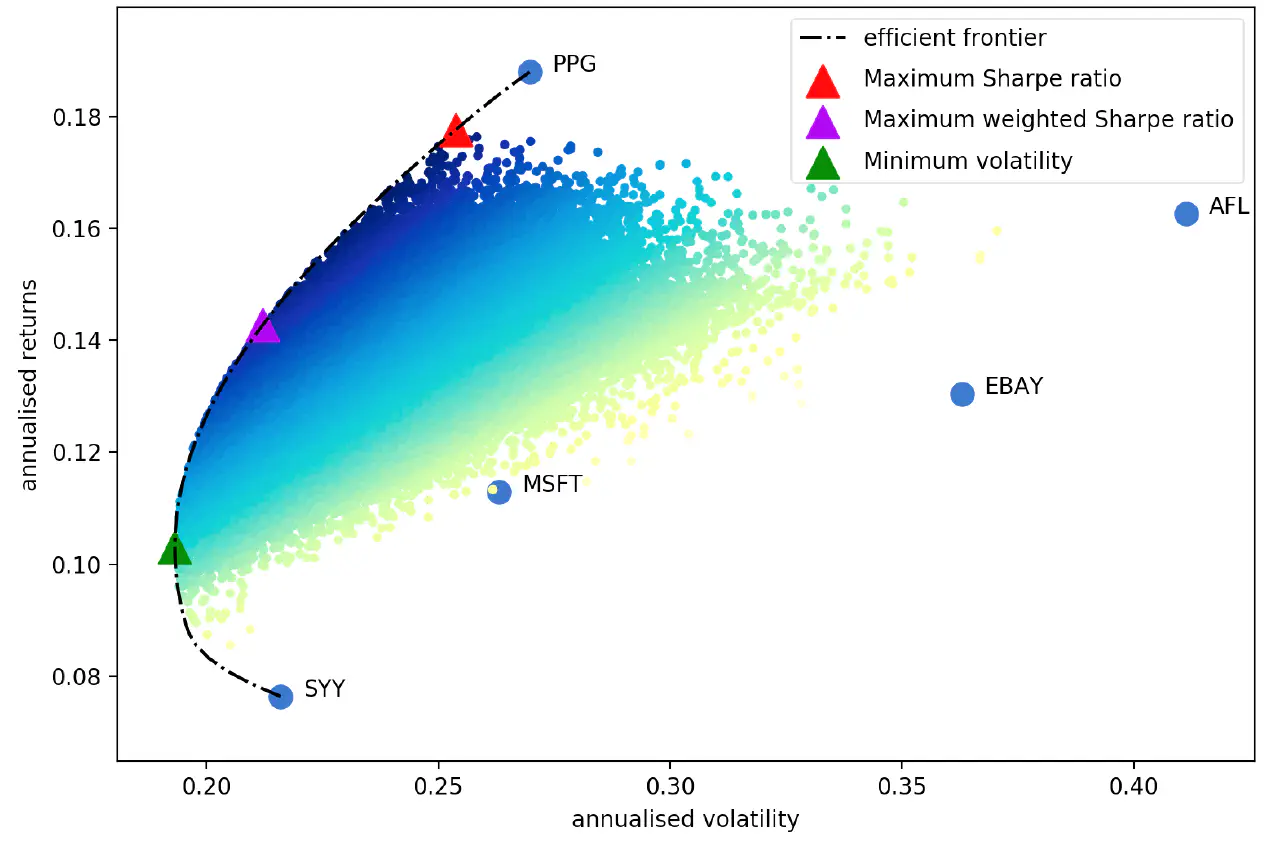
每个蓝色的点代表单个资产,横轴纵轴分别表示波动(returns)和收益(volatility)。
通过组合资产占比,获得大量的采样点,而这些采样点形成了一个等高线(efficient frontier),等高线右下角的区域是无需考虑的,因为他们要么同等收益,波动更大,要么同等波动,收益更小。
用这个等高线,我们可以开始选自己的目标了。
- 最大收益:选最上面的点(图中PPG,是个资产,也是线上一点)
- 最小波动:选最左边的点(图中绿色)
- 最大sharp ratio:选等高线和 \(y=x+b\) 的切线(图中红色,斜率为1的线图中未画出)
一些实验
格雷厄姆在《聪明的投资者》中介绍了50:50的股债平衡策略。
哈利·布朗在《永久投资组合》中介绍了25:25:25:25的股票、长债、黄金、短债/现金的策略。
杰里米·西格尔在《股市长线法宝》中介绍了红利再投资的策略。
(本来觉得bitcoin应该也加进去的,发现结果太离谱。。。所以先不加了)
我们选择如下资产(都已经做了分红处理,没有加入短债/现金):
| symbol | 描述 | 备注 |
|---|---|---|
| 510300.SS | 上证300 | 大公司 |
| 510500.SS | 中证500 | 小公司 |
| 510880.SS | 上证红利 | 高分红 |
| 511010.SS | 中国国债 | 长期国债 |
| IAU | 黄金 | 贵金属 |
| QQQ | 纳斯达克100 | 科技公司 |
| SPY | 标普500 | 大公司 |
| IVZ | 美国红利 | 高分红 |
| TLH | 美国国债 | 长期国债 |
实验上我们选择2015年至今(2023-07-30)。
先粗略的看一下:
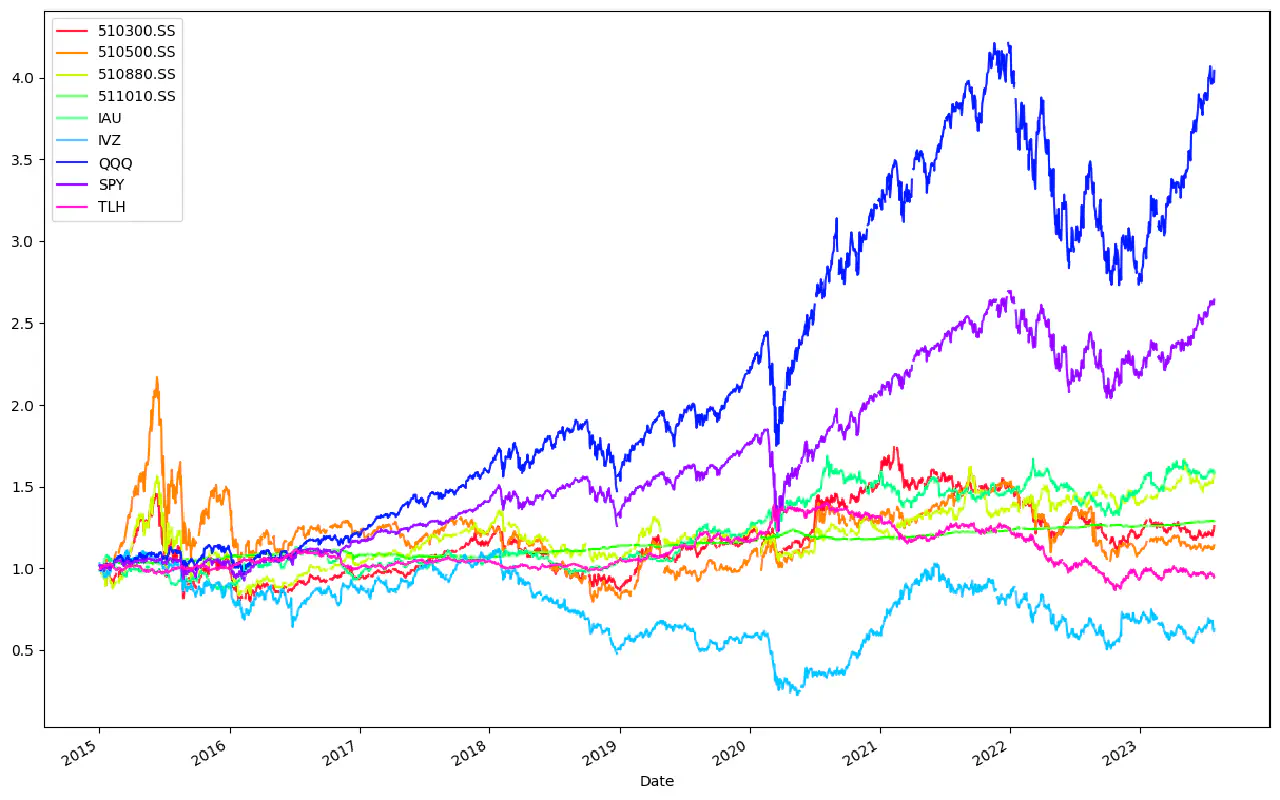
怎么说呢。。。还是不说一些主观地分析了。
再看看相关性:
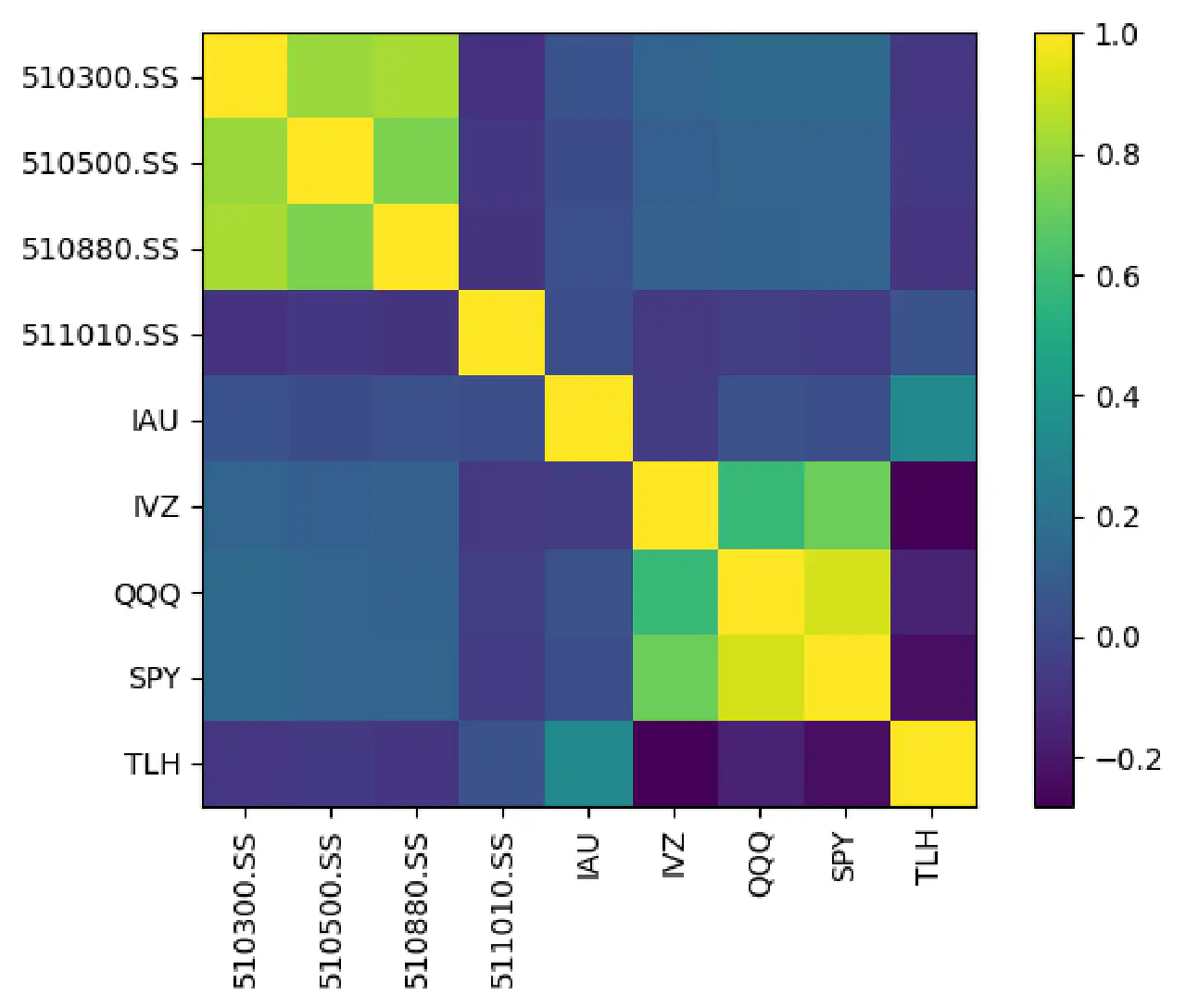
平均年回报率:
| symbol | 备注 | 年化收益 | 波动 |
|---|---|---|---|
| 510300.SS | 上证300 | 0.043697 | 0.22471600 |
| 510500.SS | 中证500 | 0.035729 | 0.27972100 |
| 510880.SS | 上证红利 | 0.057655 | 0.20632300 |
| 511010.SS | 中国国债 | 0.029760 | 0.03346700 |
| IAU | 黄金 | 0.060515 | 0.13774400 |
| IVZ | 纳斯达克100 | -0.021234 | 0.37722100 |
| QQQ | 标普500 | 0.171376 | 0.21759500 |
| SPY | 美国红利 | 0.122829 | 0.17842900 |
| TLH | 美国国债 | -0.001732 | 0.10550600 |
接下来开始计算了,portfolio 101第一题:
最小波动组合
symbol 比例 metrics performance 510300.SS 0.01005 Expected annual return 2.9% 510500.SS -0.00218 Annual volatility 3.0% 510880.SS 0.02301 Sharpe Ratio 0.31 511010.SS 0.92293 IAU 0.01881 IVZ 0.00158 QQQ -0.02801 SPY 0.07058 TLH 0.08332 最大sharp ratio
symbol 比例 metrics performance 510300.SS -0.14312 Expected annual return 15.2% 510500.SS -0.08051 Annual volatility 11.4% 510880.SS 0.25929 Sharpe Ratio 1.15 511010.SS 0.80922 IAU 0.19586 IVZ -0.27263 QQQ 0.41713 SPY 0.18781 TLH -0.37304
- 波动率<10%情况下,最大收益
symbol 比例 metrics performance 510300.SS 0.0 Expected annual return 9.5% 510500.SS 0.0 Annual volatility 10.0% 510880.SS 0.03241 Sharpe Ratio 0.75 511010.SS 0.35599 IAU 0.1854 IVZ 0.0 QQQ 0.4262 SPY 0.0 TLH 0.0
- 最后,画出等高线
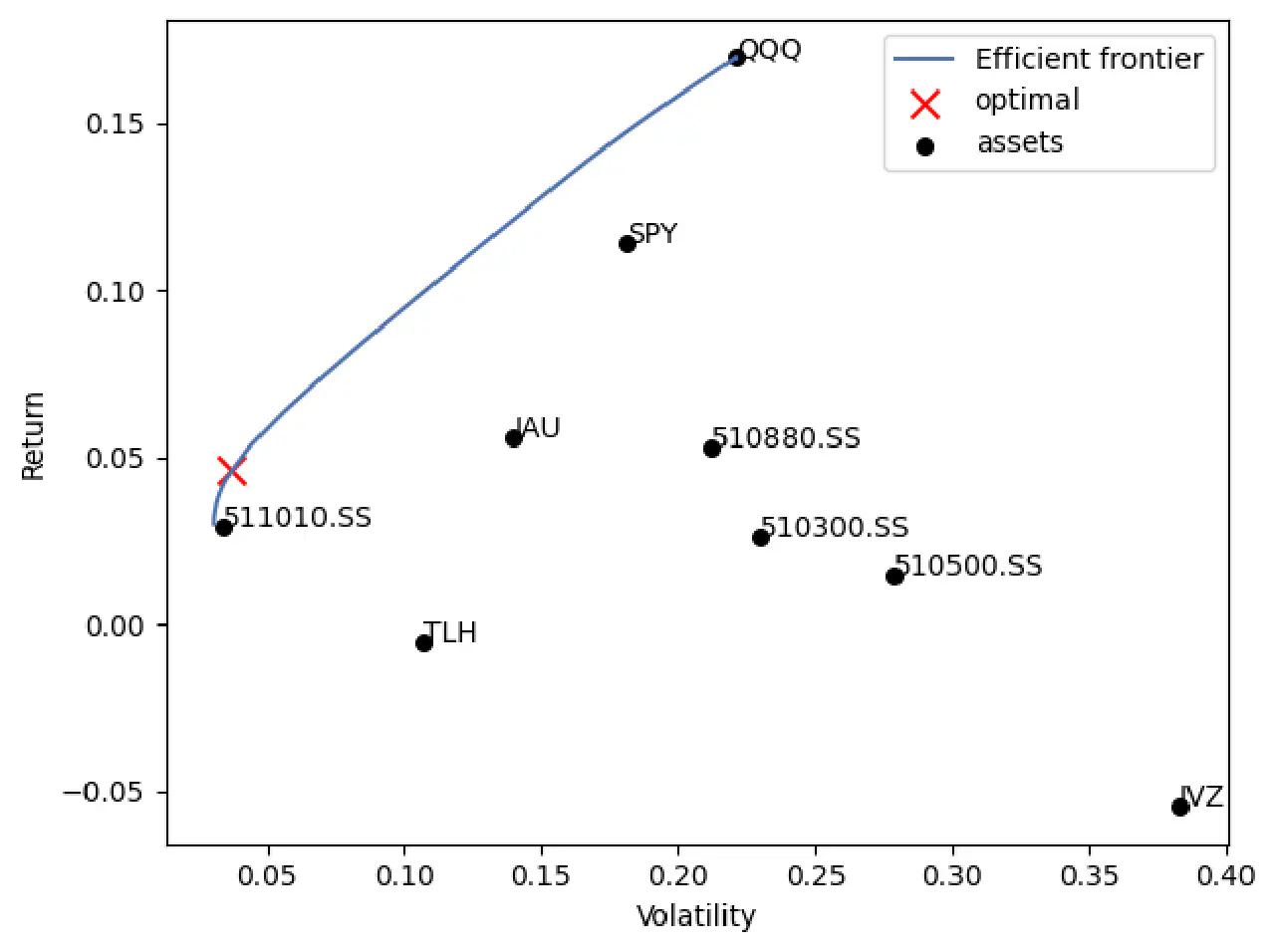
其实上面的问题都可以从这个图看出来。
future work
很可惜没有得到什么银弹结论。
希望有更深理解的人可以指导我一下。
其实应该加一些动态策略,比如周期性平衡什么的,先TODO着。